GMAT Problem Solving - The Figure Shown Above Consists of a Shaded 9-Sided Polygon

Question:

The figure shown above consists of a shaded 9-sided polygon and 9 unshaded isosceles triangles. For each isosceles triangle, the longest side is a side of the shaded polygon and the two sides of equal length are extensions of the two adjacent sides of the shaded polygon. What is the value of a?

1. 100
2. 105
3. 110
4. 115
5. 120

“The figure shown above consists of a shaded 9-sided polygon and 9 unshaded isosceles triangles.” - this is a topic of the GMAT Quantitative reasoning section of GMAT. This question has been taken from the book "GMAT Official Guide Quantitative Review". To solve GMAT Problem Solving questions a student must have knowledge about a good number of qualitative skills. The GMAT Quant section consists of 31 questions in total. The GMAT quant topics in the problem-solving part require calculative mathematical problems that should be solved with proper mathematical knowledge.

Solution and Explanation:

Approach Solution 1:

Generally, in an n-sided polygon, the sum of their internal angles is (n-2)*18°
The above question states that the given polygon is 9-sided. So, the sum of internal angles is 7*180°, making each of the individual angles 7*180°9=140°
Let the two angles be a, b, and c.
Since we know that in isosceles triangles two sides are of equal length,
Then we have two cases:
Case 1. b=c (angles opposite equal sides are equal in magnitude)
Case 2. a+b+c =180° (sum of angles in a triangle is 180 degrees)
Therefore, the sum of the angles in a straight line is 180°, b+140 = 180°.
Thus b = c = 40°
Using this data in a+b+c =180°, we can conclude that a = 100
Therefore Option A is the required correct answer.

Correct Answer: A

Approach Solution 2:

In a 9-sided polygon, the sum of the interior angles of the polygon is 180(9 – 2) = 1260 degrees

Let us check the diagram given below to understand the question.
Let the base angles of the isosceles triangle with vertex angle be labeled here as “a” degrees be x degrees. So, the interior angles of the polygon adjacent to these base angles be 180 – x degrees. 
Two interior angles are supplementary to the base angle of the isosceles triangle it is adjacent.

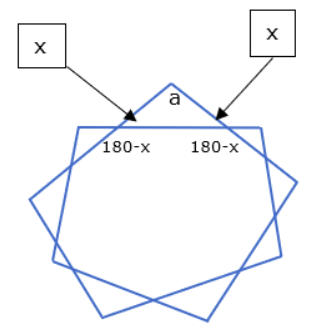
Now the base angle of x degrees is a vertical angle with the base angle of its adjacent isosceles triangle. So the base angle is also x degrees. 

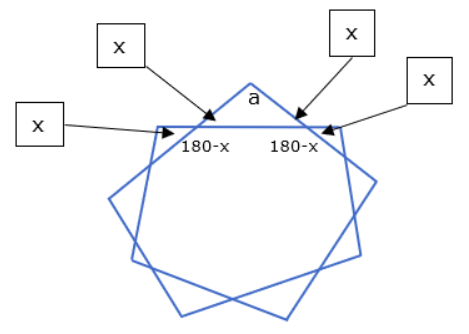
The base angles of all isosceles triangles are x degrees. All interior angles of the polygon are 180 – x degrees.

Hence, each interior angle of the polygon is equal to 1260/9 = 140 degrees.
So, 180 – x = 140, x = 40 degrees = base angle of each isosceles triangle.
Since a is the degree measure of the vertex angle of the isosceles triangle is a = 180 – 2(40) = 100 degrees.

Correct Answer: A

Approach Solution 3:
It is given in the question as a 9-sided polygon. We can consider the unshaded part as an isosceles triangle.
So, as the properties of an isosceles triangle, it can be stated that the red dots are equal.

The next angle over is opposite the angle with the red dot. The properties of the isosceles triangle also suggest that the angle is also equal to the other two angles as given in the diagram below.

Since the next triangle is an isosceles triangle, its other angle is equal to the first as given in the diagram below.

Applying the same rules and logic to see that all of the red dotted angles are all equal as given in the diagram below.

In case, all of the red-dotted angles are equal. Then all of the angles denoted with x are all equal, as given in the diagram below.

To get the value of x, we can use the rule given-below:
the sum of the angles in an n-sided polygon = \(\frac{n-2}{180°}\)
So, in a 9-sided polygon, the sum of all 9 angles =\(\frac{9-2}{180°}\) = \(\frac{7}{180°}\)°
So, each angle =\(\frac{\frac{7}{180°}}{9}\) = 140°
So, the red-dotted angle is on the line with the 140°, the red-dotted angle = 40°
Adding this data to the diagram below:

As mentioned that the unshaded triangle is isosceles, and the other angle is also 40°

Since all three angles in the triangle must add to 180°, the last remaining angle (a°) is 100°
Therefore Option A is the required correct answer.

Correct Answer: A

Suggested GMAT Problem Solving Questions

• ​GMAT Problem Solving- Is Square Root = Always Positive? 
• ​GMAT Problem Solving- Following equations has a solution in common with x^2 - 2
• ​GMAT Problem Solving- What is the units digit of the product (32^28) (33^47) (37^19)?
• ​GMAT Problem Solving- Is Zero Even Integer or Odd Integer?
• GMAT Problem Solving- How many even divisors of 1600 are not multiples of 16?
• ​GMAT Problem Solving- How many 5 digit (digit = 0 - 9) zip codes can exist in which at least one digit is repeated ?
• ​GMAT Problem Solving- How Much is the Greatest of Five Consecutive Even Integers Greater than the Smallest? 
• ​GMAT Problem Solving- The least number of digits (including repetitions) needed to express 10^100 in decimal notation
• ​GMAT Problem Solving- largest 3 digit number to have an odd number of factors
• GMAT Problem Solving- Bag A Contains Red, White and Blue Marbles such that
• ​GMAT Problem Solving- Greg Assembles Units of a Certain Product at a Factory. 
• ​GMAT Problem Solving- A Scientific Research Study Examined a Large Number of Young Foxes
• ​GMAT Problem Solving- The Smallest of Six Consecutive Odd Integers Whose Average (arithmetic mean) is x + 2
• ​GMAT Problem Solving- The Greatest 6-Digit Number When Divided by 6, 7 ,8 , 9, and 10 Leaves a Remainder of 4, 5, 6, 7, and 8
• ​GMAT Problem Solving- If 20 Men or 24 Women or 40 Boys can do a Job in 12 Days​
• ​GMAT Problem Solving- If 10 millimeters equal 1 centimeter, how many square centimeters does 1 square millimeter equal?
• ​GMAT Problem Solving- How many Terminating Zeroes does 200 Have? 
• ​GMAT Problem Solving- Properties of Circle
• ​GMAT Problem Solving- If 10, 12 and ‘x’ are Sides of an Acute Angled Triangle, How Many Integer Values of ‘x’ are Possible?
• ​GMAT Problem Solving- For How Many Values of k is 12^12 the Least Common Multiple