If Each Side of Parallelogram P has Length 1, What is the Area of P? GMAT Data Sufficiency

Question: If each side of parallelogram P has length 1, what is the area of P ?

1. One angle of P measures 45 degrees.
2. The altitude of P is 2/2

1. Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
2. Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
3. BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
4. EACH statement ALONE is sufficient.
5. Statements (1) and (2) TOGETHER are not sufficient.

“If each side of parallelogram P has length 1, what is the area of P?”- is a topic of the GMAT Quantitative reasoning section of GMAT. This question has been taken from the book "GMAT Official Guide 2021". GMAT Quant section consists of a total of 31 questions. GMAT Data Sufficiency questions consist of a problem statement followed by two factual statements. GMAT data sufficiencycomprises 15 questions which are two-fifths of the total 31 GMAT quant questions.

Approach Solution 1:

Let us look at the diagram below:

If each side of parallelogram P has length 1, we need to find what is the area of P ?
We are looking at a RHOMBUS. The area would depend on an angle..
opposite angles are EQUAL and the sum of two angles is 180.
So just knowing one angle is sufficient

Statement 1 says One angle of P measures 45 degrees.

So, when we draw an altitude, it becomes an isosceles right angled triangle with hypotenuse as 1, so altitude=side.

=> \(s^2+s^2 = 1^2\)
=> \(s^2\) = ½

Or side = altitude =\(\sqrt2/2\)

Hence, the area is 1*\(\sqrt2/2\) = \(\sqrt2/2\)

The statement 1 alone is sufficient.

Statement 2 says: The altitude of P is \(\sqrt2\)/2

Hence, the area is 1*\(\sqrt2/2\) = \(\sqrt2/2\)

The statement 2 alsone is sufficient.
Since both the statements are sufficient alone.

Correct Answer: D

Approach Solution 2:

Since we are given a parallelogram with all equal sides, it’s actually a rhombus and we need to determine the area of the rhombus.

Statement One Alone:

One angle of P measures 45 degrees.
This is enough to determine the area of P. For example, we can draw a diagonal that doesn’t intercept the 45-degree angle and create two congruent triangles, each with two sides of length 1 and the included angle of 45 degrees. Knowing two sides and an included angle is sufficient to determine the area of the triangle since that triangle is unique. Multiplying that area by 2 will give us the area of the parallelogram/rhombus.

So statement one alone is sufficient to answer the question.

Statement Two Alone:

The altitude of P is √2/2.

The information in Fact 2 requires a bit more work, but we can now draw 2 RIGHT triangles "inside" the parallelogram. Each of those right triangles would have a hypotenuse of 1 (since the side lengths are 1s) and a 'height' of √2/2. We could determine the exact value of the 3rd side and the two angles (it ends up being a 45/45/90 right triangle), so we can then determine the area of the overall shape.
This is enough to determine the area of P. Since one side of P can be used as the base of the parallelogram/rhombus, knowing the altitude/height of P allows us to find the area;

base x height = 1 x √2/2 = √2/2
Hence, statement 2 is sufficient.

Since both the statements are sufficient alone

Correct Answer: D

Approach Solution 3:

Steps 1 & 2: Understand Question and Draw Inferences

In this question, we are given

• Each side of the parallelogram P has length 1.

We need to determine

• The area of the parallelogram P.

To determine the area of the parallelogram, we need to know the base (which is given as 1), and the height of the parallelogram.

• Hence, in this case, we need to know the height of the parallelogram only.

With this understanding, let us now analyze the individual statements.

Step 3: Analyse Statement 1

As per the information given in statement 1, one angle of P measures 45 degrees.

Hence, we can draw the parallelogram as shown:

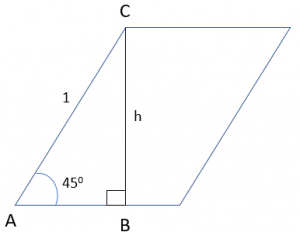
• △ABC is a right-angled triangle as shown.
  • By applying the property that sum of all angles of the triangles is 180⁰, we can say:
    • 90⁰ + 45⁰ + ∠ACB = 180⁰
    • ∠ACB = 45⁰
  • Hence, △ABC is a 45- 45 – 90 triangle.
  • Per our conceptual understanding, the side ratio in a 45 -45 -90 is 1: 1: √2.
    • Thus, BC = h = √2.
  • We can find out the area of the triangles.

Hence, statement 1 is sufficient to find the answer to the question.

Step 4: Analyse Statement 2

As per the information given in statement 2, the altitude of P is √2/2.

• Hence, h = √2/2 =√2.
• We can find out the area of the triangles.

Hence, EACH statement ALONE is sufficient.

Correct Answer: D

Suggested GMAT Data Sufficiency Questions 

• If x and y are positive integers, is x odd?​ GMAT Data Sufficiency 
• If 0 < x < 53, what is the value of integer x? ​ GMAT Data Sufficiency 
• What is the value of 6x^2 + 9y^2 =?​ GMAT Data Sufficiency 
• If x and y are integers and, is x=(y/5 +2) even? GMAT Data Sufficiency 
• If m is a positive integer, is √m>25?​ GMAT Data Sufficiency 
• If there are 78 people working at an office, how many of them are women older than 40?​ GMAT Data Sufficiency 
• If ab = ac is b = 2? GMAT Data Sufficiency 
• If x is a positive integer, what is the value of x?​ GMAT Data Sufficiency 
• If 53 students are enrolled in both the CS103 (Algorithms and Data Structures) And M101 (Mathematics for Computer Science) classes GMAT Data Sufficiency 
• Buster leaves the trailer at noon and walks towards the studio at a constant rate of B miles per hour.​ GMAT Data Sufficiency 
• If sq rt{3+sq rt(x-1)} = 4, what is the value of x? ​GMAT Data Sufficiency 
• What is the sum of a, b, and c? GMAT Data Sufficiency 
• What is the probability of getting a jack from a 52-card deck on both the first and second draw if the cards are not replaced? GMAT Data Sufficiency 
• Is P – 1 even? GMAT Data Sufficiency 
• Is the average of a set of 5 distinct positive integers {a, b, 6, 4, 2} greater than the median? GMAT Data Sufficiency 
• If a, b, and c are distinct positive integers, is (a/b)/c an integer? GMAT Data Sufficiency 
• If |m + 4| = 2, what is the value of m?​ GMAT Data Sufficiency 
• If a > b, how much greater than b is a?​ GMAT Data Sufficiency 
• What is the radius of the circle above with center O? GMAT Data Sufficiency 
• The cardinality of a finite set is the number of elements in the set. What is the cardinality of set A ? GMAT Data Sufficiency